Study Overview

In the basic RNN, the vanishing gradient problem limits a language model’s memory; a range of models, such as LSTM and GRU, have been developed to reduce this friction. In order to preserve long-term memory, these models must determine which information to store from previous hidden states. This introduces a related problem–if the model chooses the wrong information to carry in its long-term memory, it may be difficult to recover. As Kraus et al. explain,

“If the RNN’s hidden representation remembers the wrong information and reaches a bad numerical state for predicting future sequence elements, for instance as a result of an unexpected input, it may take many time-steps to recover” (Kraus et al. 2017)

This paper contributes to a small body of existing work focused on developing new architectures to improve RNN performance on modeling long-range dependencies; that is, to help RNNs remember the right information. Our goal is to assess whether a second-order LSTM – an LSTM that routes different inputs to different LSTM cells – can make progress in this research area.

Approach

Our project is divided into two stages, a proof-of-concept and an application to natural language. The proof-of-concept uses synthetic language, specifically the family of m-bounded Dyck-k (in this case, Dyck-2) languages. The second stage of the project extends the analysis to natural language, where successful modeling of long-distance dependency is more difficult to quantify.

Baseline

This baseline model consists of a single layer LSTM and the hidden states at each time step are passed through a fully connected layer to generate the predicted probability distribution across all vocabulary words.

Second-Order Model

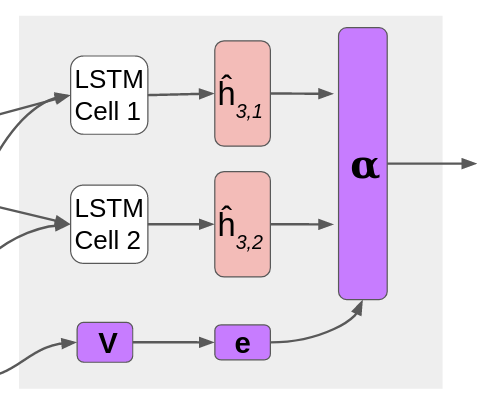
An $S$-dimensional second-order model contains $S$ LSTM cells, with $4S$ transition matrices. In the attention-based second-order LSTM model, the attention mechanism sends each input to all LSTM cells, and uses learned attention scores to compute a linear combination of the hidden and cell state outputs. Specifically, an $S$-dimensional second-order LSTM has attention matrix V with dimension $S \times embedding\_dim$. For each of the LSTM cells, we compute the intermediate hidden state and memory cell state $h_t$ and $c_t$ (represented in the figure above as joint $\widehat{h}_t$), and then use attention to compute a linear combination of the intermediate states to get the new states $h_t$ and $c_t$, as follows:

$\begin{align} &e_t = V x_t \\ &\alpha_t = \text{softmax}\left(\frac{e_t}{\tau}\right) \\ &h_t^{(s)}, c_t^{(s)} = \text{LSTMCell}^{(s)}(x_t, (h_{t-1}, c_{t-1})) \\ &h_{t} = \sum_{s=1}^{S} \alpha_{t, s} \cdot h_t^{(s)} \\ &c_{t} = \sum_{s=1}^{S} \alpha_{t, s} \cdot c_t^{(s)} \end{align}$

where $\tau$ is a temperature parameter that affects the outcome of the softmax function. Temperature is initialized “hot” with $\tau = 1$ (making (b) effectively a normal softmax), but then decreases with each epoch by a constant multiplier. The smaller the value of $\tau$, the more probability mass is put on one LSTM cell. When $\tau \approx 0.1$, (b) is effectively one-hot. We decay the temperature throughout training so that eventually each input word gets assigned to one particular LSTM cell and the hidden state output by that cell is effectively the next hidden state.

Experiments

Data

The $m$-bounded Dyck-$k$ data are comprised of $k$ unique types of parentheses, with at most $m$ unclosed parentheses appearing at any time. This formal language is useful as a proof of concept because the relationship between an open parenthesis and its corresponding close parenthesis is well-defined. This allows us to test our model’s ability to predict long-term dependencies. The data for $m = 4, 6, 8$ was provided by John Hewitt. The training datasets and test datasets each contain 10,000 samples, and the validation datasets contain 4,000 samples.

The WikiText-2 dataset, which contains 2 million training tokens and a vocabulary of 33k words, is publicly available. We use this data to test our model’s performance on natural language modeling tasks. For the natural language model, we load the raw data as a continuous stream; the sequence length is determined by the BPTT parameter, and the batches are constructed so that the hidden state is transferable from one batch to the next. Specifically, each index in a batch is a continuation of the same index in the previous batch.

Evaluation method

We use two quantitative evaluation metrics, perplexity and parenthesis prediction accuracy. The formula for parenthesis prediction accuracy is from John Hewitt. The prediction accuracy is measured only for close parentheses, since there is no reason to favor one open parenthesis over another. A prediction is considered correct if at least 80% of the probability mass on any close parenthesis is placed on the true close parenthesis. The distance between an open parenthesis and its corresponding close parenthesis is called closing distance. The long distance prediction accuracy (LDPA) is calculated separately for each possible closing distance. We also report the worst-case prediction accuracy (WCPA), which is the minimum prediction accuracy over all distances.

Results

Table 1 shows that the attention model achieves marginally lower perplexity than the baseline model across $m4$, $m6$, and $m8$. The attention model slightly under-performs relative to the baseline model on WCPA for the $m4$, but performs slightly better on the test set for $m6$ and $m8$.

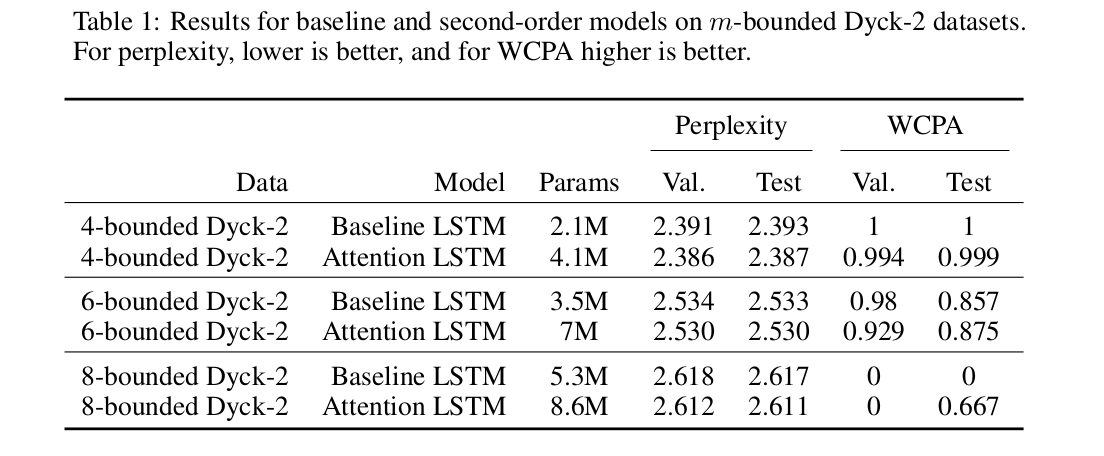
Overall, the attention model performs similarly to the baseline model on the synthetic data. Although it did not show quantitative improvement over the baseline, our attention model is much more stable during training than the baseline model. The validation WCPA for the baseline model oscillates drastically throughout training but WCPA for the attention model does not. The attention model also trains in fewer epochs than the baseline model.

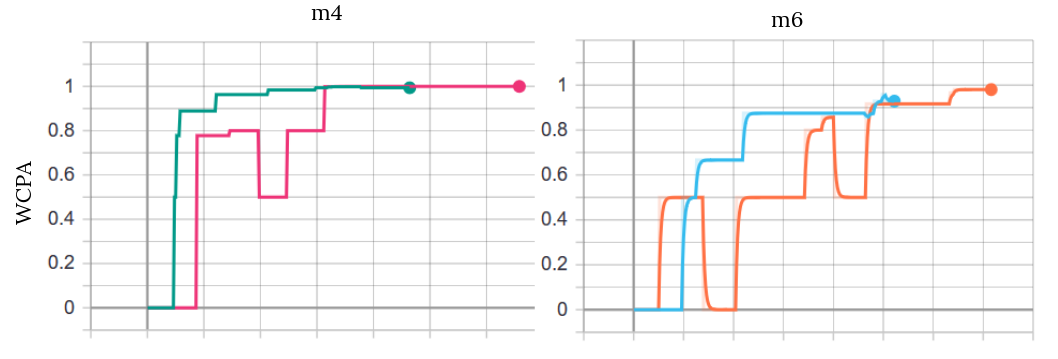
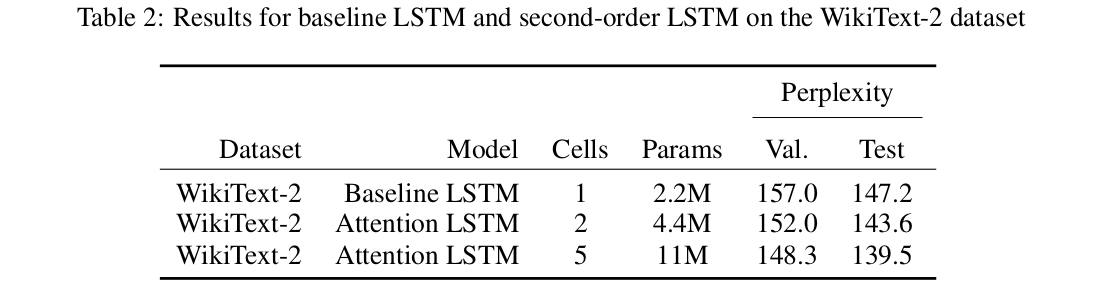
Table 2 shows the validation and test results on the WikiText-2 dataset. The attention model with 2 cells and 5 cells both outperform the baseline single-cell model by a significant margin. We suspect the attention model is able to perform better on the WikiText-2 dataset than the parentheses dataset because there are more intricate dependencies between words. The long-distance relationship between parentheses can be captured by just a stack, whereas the relationship between words are harder to capture. It is also possible that the the significant increase in the number of parameters between the baseline and the attention model is responsible for the improved performance.

Analysis

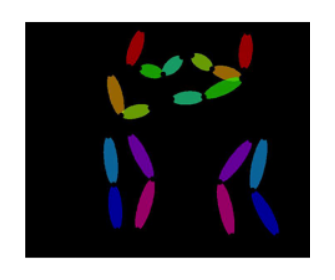
In order to capture the differentiation of the LSTM cells in the second-order models, we created heatmaps of sample sentences. The color of the word indicates which LSTM unit was assigned the largest attention score, $s^* = \arg\max_s \alpha_{t,s}$, and the intensity of the color reflects the magnitude of $\alpha_{t, s^*}$. Sample heatmaps for both the formal and natural languages are shown below. The heatmap for the formal language shows that all open parentheses are assigned to one LSTM unit, and all closed parentheses are assigned to the other. This pattern was contrary to our expectations; we expected the two LSTM units to each store the stack for one type of parentheses. However, if the inputs are grammatically correct, a closed parentheses will always indicate a pop from the stack and an open parentheses will always indicate a push to the stack. Therefore, it seems reasonable that one LSTM unit encodes “pop” and the other encodes “push.”

The pattern for the natural language heatmap is less discernible. There is no pattern with regard to part of speech or word order within the sentence. The attention is consistent in that individual words are always (softly) assigned to the same cells. Some phrases, like “first down” and “fourth down,” are also highlighted consistently. It is possible that a larger number of LSTM units, a larger training set, or fine-tuning of the model parameters would yield a more interpretable pattern. Future work could explore the parameters that yield the best differentiation.

Discussion

Overall, the performance of the attention-based second-order LSTM was comparable to the baseline. The attention-based model training on the $m$-bounded Dyck-$k$ dataset learned LDPA and WCPA more quickly and stably than the baseline and trained in fewer epochs. On the WikiText-2 dataset, the attention-based second-order LSTM achieved lower perplexity than baseline (139.5 for 5 hidden cells and 143.6 for 2 hidden cells, compared to 147.2 baseline). However, the parameters are not shared between cells within the attention model, so the attention models contain more parameters than the baseline LSTM.

The primary limitation of this work is that it is limited to LSTM architectures. Ideally, we would have compared a second-order RNN model to a baseline RNN as well as the baseline LSTM. This would allow us to assess whether the second-order model is useful for the parenthesis prediction task; this was difficult to assess with only an LSTM because the baseline LSTM works so well in practice.

Future work in this area could explore how training data size, model size, and parameter tuning (particularly the number of LSTM units) impact model performance.